- Notation cartésienne, plan complexe
- Module et distance dans le plan complexe
- Trigonométrie circulaire
- Forme trigonométrique (polaire)
- Équation du second degré dans ℂ
- Racines n-ièmes dans ℂ
- Exponentielle complexe
- Interprétations géométriques
Racines n-ièmes de l’unité
Dans tout cette sous-section, on désigne par {n} un entier strictement positif.
Définition
On appelle racines {n}-ièmes de l’unité les solutions dans {\mathbb{C}} de l’équation {z^{n}=1}.
On note {\mathcal{U}_{n}} l’ensemble des racines {n}-ièmes de l’unité.
On appelle racines {n}-ièmes de l’unité les solutions dans {\mathbb{C}} de l’équation {z^{n}=1}.
On note {\mathcal{U}_{n}} l’ensemble des racines {n}-ièmes de l’unité.
Proposition
L’ensemble {\mathcal{U}_{n}} des racines {n}-ièmes de l’unité est formé de {n} nombres complexes distincts.
Les éléments de {\mathcal{U}_{n}} sont donnés par par {\omega_k=\text{e}^{2ik\pi/n}}, avec {0\le k\le n -1}.
Si on note {\omega=\omega_1=\text{e}^{2i\pi/n}}, alors {\omega_k=\omega^k} pour tout {k} (en particulier {\omega_0=1}).
Autrement dit, avec ces notations: {\mathcal{U}_{n}=\{1,\omega,\omega^2,\ldots,\omega^{n-1}\}}.
L’ensemble {\mathcal{U}_{n}} des racines {n}-ièmes de l’unité est formé de {n} nombres complexes distincts.
Les éléments de {\mathcal{U}_{n}} sont donnés par par {\omega_k=\text{e}^{2ik\pi/n}}, avec {0\le k\le n -1}.
Si on note {\omega=\omega_1=\text{e}^{2i\pi/n}}, alors {\omega_k=\omega^k} pour tout {k} (en particulier {\omega_0=1}).
Autrement dit, avec ces notations: {\mathcal{U}_{n}=\{1,\omega,\omega^2,\ldots,\omega^{n-1}\}}.
Cas particuliers
- La seule racine « une-ième » de l’unité est {z=1} (donc {\mathcal{U}_{1}=\{1\}}).
- Les deux racines carrées de l’unité sont {1} et {-1} (donc {\mathcal{U}_{2}=\{1,-1\}}).
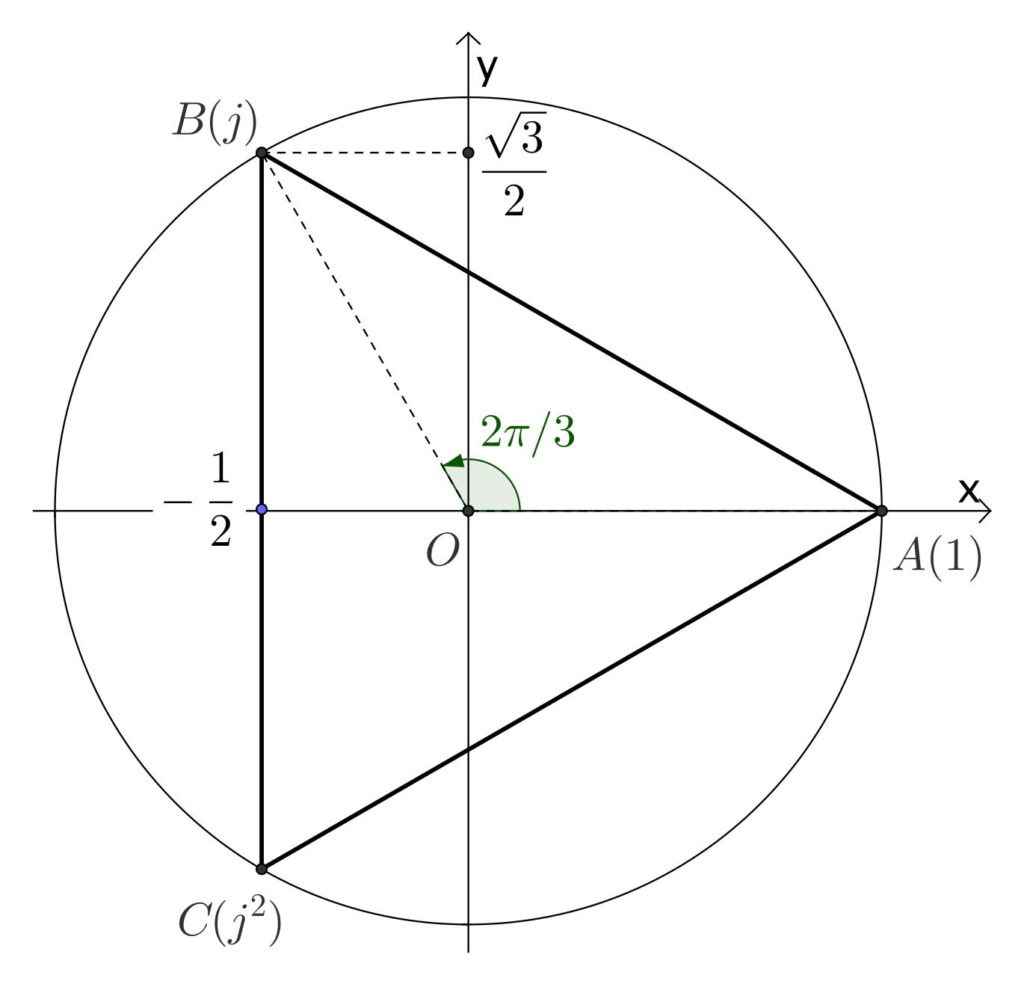
- Les trois racines cubiques de l’unité sont {1,j,j^{2}} avec {j=\text{e}^{2i\pi/3}} (donc {\mathcal{U}_{3}=\{1,j,j^{2}\}}).
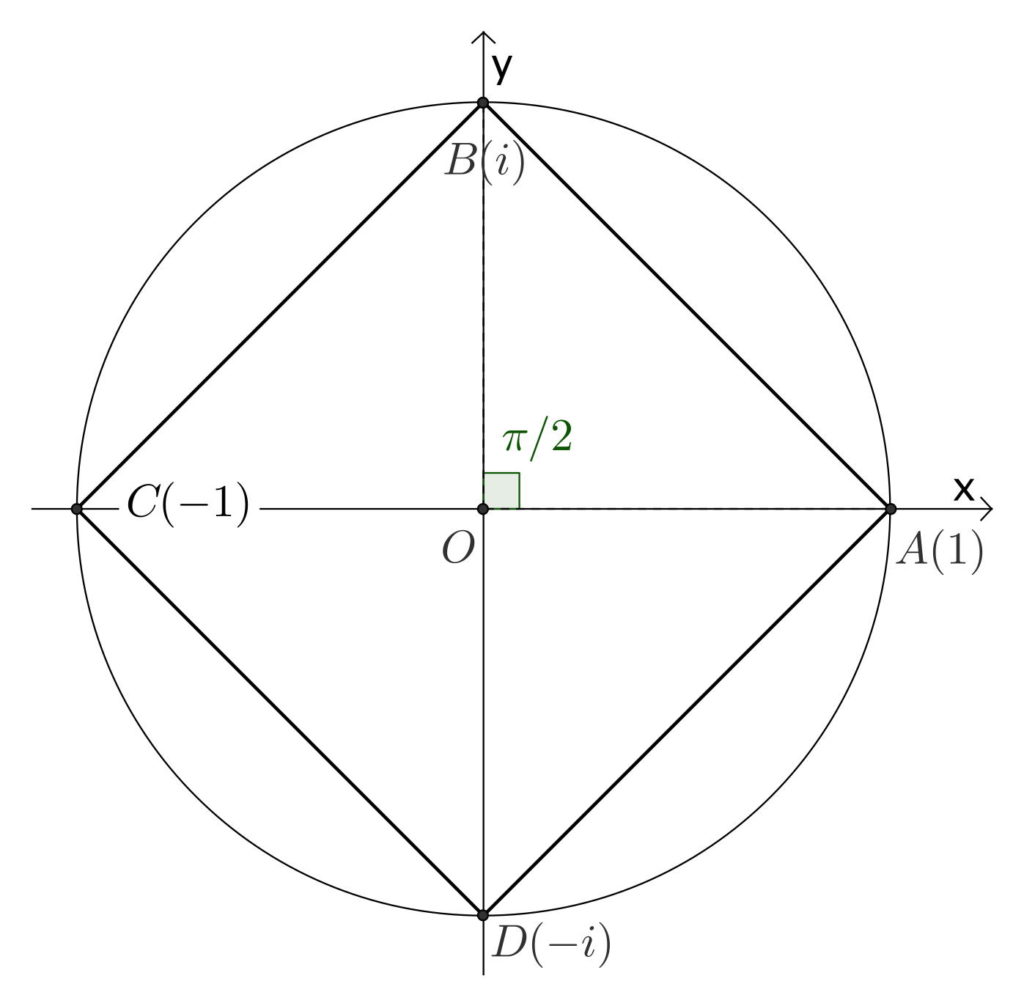
- Les racines quatrièmes de l’unité sont: {1,i,-1,-i} (donc {\mathcal{U}_{4}=\{1,i,-1,-i\}}).
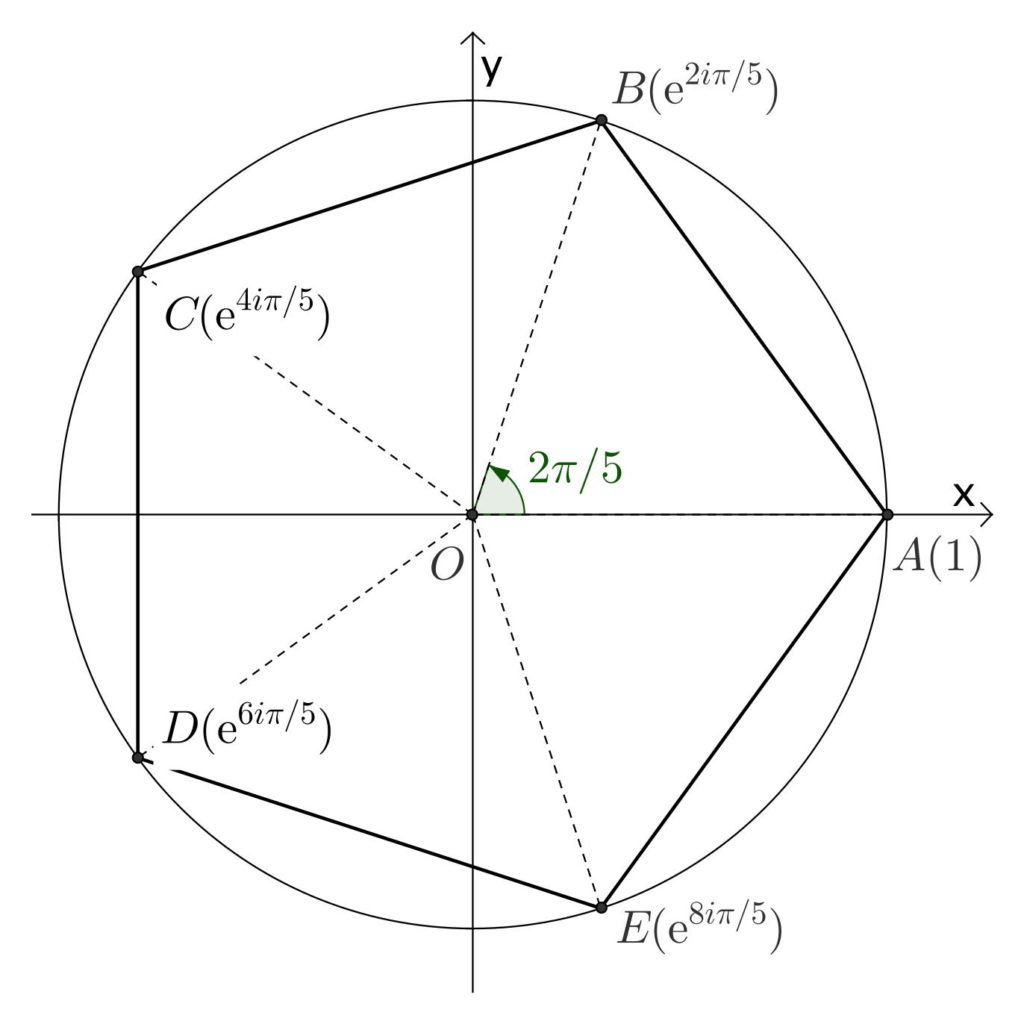
- Les racines cinquièmes de l’unité sont {1,\omega,\omega^2,\omega^3,\omega^4}, avec {\omega=\text{e}^{2i\pi/5}}.
- Les racines sixièmes de l’unité sont : {1,\text{e}^{i\pi/3}=-j^{2},\ j,\ -1,\ j^2}, et {-j}.
Proposition (disposition dans le plan complexe)
Les points images des racines {n}-ièmes de l’unité forment les {n} sommets d’un polygône régulier convexe inscrit dans le cercle unité, l’un de ces sommets étant le point d’affixe {1}.
Racines cubiques de l’unité :Les points images des racines {n}-ièmes de l’unité forment les {n} sommets d’un polygône régulier convexe inscrit dans le cercle unité, l’un de ces sommets étant le point d’affixe {1}.
Racines quatrièmes de l’unité :
Racines cinquièmes de l’unité :
L’ensemble des points-images des racines sixièmes de l’unité forme bien sûr un hexagone régulier de sommet {0}, dont un sommet est {A(1)}, et on fera soi-même le dessin!
Remarques
Pour voir la suite de ce contenu, vous devez :
- avoir une souscription active sur mathprepa
- et être connecté au site
- revenir à la page d'accueil
- ou tester la page d'extraits libres
- ou consulter le plan du site
Page précédente : équation du second degré dans ℂ
Page suivante : exponentielle complexe