- Continuité uniforme
- Continuité par morceaux
- Intégrale sur un segment
- Intégrale et primitives
- Formules de Taylor
Définition de l’intégale sur un segment
Proposition (approximation par des fonctions en escaliers)
Soit {f:[a,b]\to\mathbb{R}} une fonction continue par morceaux, à valeurs réelles.
Pour tout {\varepsilon>0}, il existe deux fonctions en escaliers {\varphi} et {\psi} sur {[a,b]} telles que :
Soit {f:[a,b]\to\mathbb{R}} une fonction continue par morceaux, à valeurs réelles.
Pour tout {\varepsilon>0}, il existe deux fonctions en escaliers {\varphi} et {\psi} sur {[a,b]} telles que :
- pour tout {x} de {[a,b]}, {\varphi(x)\le f(x)\le\psi(x)}.
- pour tout {x} de {[a,b]}, {0\le\psi(x)-\varphi(x)\le\varepsilon}.
Proposition (intégrale des fonctions continues par morceaux à valeurs réelles)
Soit {f:[a,b]\to\mathbb{R}} une fonction continue par morceaux à valeurs réelles.
On considère les deux quantités suivantes :
Soit {f:[a,b]\to\mathbb{R}} une fonction continue par morceaux à valeurs réelles.
On considère les deux quantités suivantes :
- {I_{-}(f)=\displaystyle\sup_{\varphi\le f}\int_{[a,b]}\varphi}, borne supérieure sur les {\varphi} en escaliers telles que {\varphi\le f}.
- {I^{+}(f)=\displaystyle\inf_{\psi\ge f}\int_{[a,b]}\psi}, borne inférieure sur les {\psi} en escaliers telles que {\psi\ge f}.
Alors {I_{-}(f)} et {I^{+}(f)} sont des réels égaux.
Leur valeur commune est appelée intégrale de {f} sur {[a,b]}, et elle est notée {\displaystyle\int_{[a,b]}f}.
Si {f} est en escaliers, donc continue par morceaux, les deux significations de {\displaystyle\int_{[a,b]}f} coïncident.
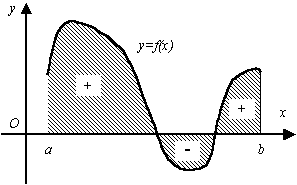
Interprétation en terme d’aire
Soit {f:[a,b]\to\mathbb{R}} une fonction continue par morceaux.
L’intégrale de {f} sur {[a,b]} représente l’aire algébrique du domaine situé entre la courbe {y=f(x)} et l’axe {Ox}, cette « aire » étant comptée positivement sur les intervalles où {f\ge0} et négativement sur les intervalles où {f\le0}. Numériquement, le résultat est exprimé en unités d’aire (ua).
Pour voir la suite de ce contenu, vous devez :
- avoir une souscription active sur mathprepa
- et être connecté au site
- revenir à la page d'accueil
- ou tester la page d'extraits libres
- ou consulter le plan du site
Page précédente : continuité par morceaux
Page suivante : intégrale et primitives