Continuité par morceaux

Plan du chapitre "Intégration"

Dans ce chapitre, ${[a,b]}$ est un segment de ${\mathbb{R}}$ et ${a\lt b}$ .

Fonctions en escaliers

Définition (subdivisions d'un segment)
On appelle subdivision de

{[a,b]}

toute suite finie

{(x_0=a\lt x_1\lt \ldots\lt x_{n-1}\lt x_n=b)}

.
L’ensemble

{\{a=x_0,\ldots,x_k,\ldots,x_n=b\}}

est appelé le support de la subdivision.
La quantité

{h=\max(x_{k+1}-x_k)}

est appelée le pas de la subdivision.

Finesse d’une subdivision

Soit ${\sigma}$ et ${\sigma'}$ deux subdivisions de ${[a,b]}$ .
On dit que ${\sigma}$ est plus fine que ${\sigma'}$ si le support de ${\sigma}$ contient celui de ${\sigma'}$ .

La subdivision notée ${\sigma\cup\sigma'}$ et dont le support est la réunion de ceux de ${\sigma}$ et de ${\sigma'}$ est plus fine que chacune des subdivisions ${\sigma}$ et ${\sigma'}$ .

Réciproquement si une subdivision de ${[a,b]}$ est plus fine que ${\sigma}$ et ${\sigma'}$ , alors elle est plus fine que ${\sigma\cup\sigma'}$ .

Définition (fonctions en escaliers sur un segment)
Soit

{\varphi}

une fonction définie sur

{[a,b]}

, à valeurs dans

{\mathbb{K}}

.
On dit que

{\varphi}

est en escaliers sur

{[a,b]}

s’il existe une subdivision

{\sigma=(x_k)_{0\,\le\,k\,\le\,n}}

{[a,b]}

et
s’il existe

{n}

scalaires

{\lambda_0,\lambda_1,\ldots,\lambda_{n-1}}

tels que :

{\forall\, k=0,\ldots,n-1,\;\forall\, t \in\;]x_k,x_{k+1}[,\;\varphi(t)=\lambda_k}

On dit alors que la subdivision

{\sigma}

est adaptée (ou encore subordonnée) à la fonction

{\varphi}

.
On note

{\mathcal{E}([a,b],\mathbb{K})}

l’ensemble des fonctions en escaliers sur

{[a,b]}

et à valeurs dans

{\mathbb{K}}

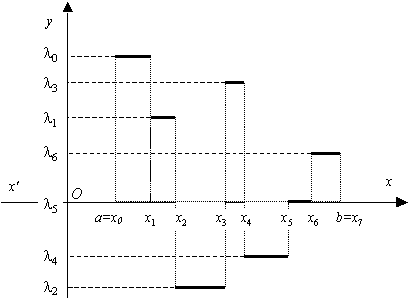
La figure ci-dessous représente une fonction en escaliers ${\varphi}$ sur le segment ${[a,b]}$ , à valeurs réelles.

On n’a pas représenté les valeurs de ${\varphi}$ aux points ${x_k}$ , car ces valeurs sont sans importance.

Pour voir la suite de ce contenu, vous devez :

avoir une souscription active sur mathprepa
et être connecté au site

Pour poursuivre votre exploration, vous pouvez :

revenir à la page d'accueil
ou tester la page d'extraits libres
ou consulter le plan du site

Page précédente : continuité uniforme
Page suivante : intégrale sur un segment